X( , ) t fijo x(t, ) es una variable aleatoria.
Si w es fijo, x( , w) es una función de t elemento de T llamada una realización o trayectoria del proceso.
Espacio de estados del proceso es el conjunto de todos los posibles valores que puede tomar la variables x(t) para toda t elemento de T.
S espacio de de estados del proceso. Donde cada punto en S en conocido como estado del proceso.
S es finito entonces el proceso es discreto.
S es un intervalo, entonces el proceso es continuo.
S son los valores que toma la variable aleatoria.
Si T es numerable X es un proceso con parámetros o tiempo discreto
SI T es un intervalo ( a,b), decimos que es un proceso con parámetros o tiempo continuo.
Si X={x(t) t E T} es discreto, entonces, T( 0,1,2,3,…) escribimos a X(t) como Xt lo cual es una sucesión de variables aleatorias.
Entonces, una serie de tiempo es la sucesión de observaciones generadas por un proceso estocástico cuyo conjunto de índices se toma en relación al tiempo. Hay series de tiempo estacionarias, es decir, que en cualquier momento que se observe, se tiene el mismo valor.
Sea N(t) el numero de clientes en un sistema de espera, entonces N(t) es un proceso en tiempo continuo (tiempo de espera) con espacio de estados discretos (numero de clientes que llegan a un sistema de espera)
Un proceso de conteo es un proceso N(t) t>0 con espacio de estados S=(0,1,2,3…) tal que para cada t>0 N(t) cuenta el numero de veces que ha ocurrido un cierto evento E durante el intervalo ( 0,E).
Es un proceso de conteo si satisface lo siguiente:
N(0) = 0
N(t) solo toma valores enteros no negativos
N(t) es no decreciente o sea N(s) <=N(t) t>=s
N(t) –N(s) es el numero de veces que el evento ocurrió en el intervalo ( s,t)
X proceso estocástico, X proceso de incrementos independientes si 0
Proceso Autorregresivos Xt=φXt-1 + ε
Para conocer el estado futuro dependo de lo que esta sucediendo en el estado actual.
Proceso de Markov es un proceso estocástico donde las distribuciones no dependen del pasado, solo del pasado inmediato o del presente, es decir, para calcular lo que pasa en n+1 solo necesito saber lo que paso en n.
Es un proceso de Markov si y solo si para cualquier entero n, y tiempo t1

Cadena de Markov en tiempo discreto sean S y T conjuntos numerables S=(xo, x1, ..xn) y T=(to,t1,t2,…tn) entonces x=[x(t), t e T] x=[xn, n=1,2,3…n] si
P[xn+1=J/xo=io,…xn-1=in-1,xn=i]= P{Xn+1=J/xn=i} para todo n y todos los estados de io,i1,…in-1,i,j
Ejemplos: problemas de inventarios, procesos autorregresivos.
Probabilidades de transición es la probabilidad de una variable pase de un estado a otro.
Para una cadena de Markov en tiempo discreto Xn, la probabilidad de que xn+1 este en el estado j dado que xn esta en el estado i se le llama la probabilidad de transición en un paso.

La matriz depende de la distribución de las probabilidades.
Si el espacio de estados de la cadena es finito (K) entonces la matriz P tiene un numero finito de columnas y renglones (K x K)
Las probabilidades de transición satisfacen las siguientes características:
Pij > 0 para toda i y j
ΣPij =1
Si el proceso llega a un estado donde la probabilidad Pij=1 el proceso ya no se mueve y a este lo llamamos un proceso absorbente.
Una cadena de Markov esta bien definida si conozco su estado inicial y su distribución.
Generalmente el proceso va de un estado a otro en una sucesión de pasos:
Pn=Pij(n) en donde Pij(n)= P{Xn=j/Xo=i}=P{Xn+m=j/ Xm=i} para toda m>0 ir del estado i en t=m al estado j en n pasos ya no es homogéneo ya depende de n.
Las probabilidades de transición de una cadena de Markov en n pasos satisface que:

Si pi=qi=P entonces ri=1-2P para toda i 1>…..j P>0
Se dice entonces que Xn es una caminata aleatoria simétrica
Si pi=qi y ri =0 (no se puede quedar en el mismo estado) entonces qi=pi= ½ se dice que Xn es una caminata aleatoria simple
Ejemplo:
En cualquier día Pedro puede estar Feliz (f), deprimido (d) o ninguno de los dos (I).
Si hoy esta Feliz mañana estará f, d, i con probabilidad de .5,.4, .1; si pedro esta d, entonces estará mañana f, d, i, con probabilidad de .3, .4, .3 y si hoy esta indiferente, entonces mañana estará f, d ,i con probabilidad de .2, .3, .5
La Matriz es:

donde la diagonal es la probabilidad de que se quede en el mismo estado.
Cadena de Markov Irreducible
Sean i y j estados de una cadena de Markov Xn, decimos que j es alcanzable desde el estado i si Pij^(n)>0 para alguna n>0; es decir se puede ir del estado i al estado j en algún numero finito de n pasos. Y se escribe i -> j; si también i es alcanzable desde j entonces decimos que i y j son estados comunicantes.( i<->j)
i<->j es una relación de equivalencia:
Reflexiva i<->i
Simétrica i<->j si y solo si j<->i
Transitiva i<->j entonces j<->k entonces i<->k
El espacio de estados S de la cadena se puede particionar en clases de equivalencia o sea subconjuntos c1, c2,… donde la intersección de 2 subconjuntos es distinta del vacío y la unión de todos los ci es igual a S
Conociendo las clases de equivalencia se conocen las rutas que siguen el proceso. 2 estados comunicantes pertenecen a la misma clase. Si S tiene un solo subconjunto entonces el proceso visita todos los estados.
Periodo: va a un estado y regresa al mismo lugar en el mismo número de pasos.
Recurrencia: sale del estado inicial llega al estado j en k pasos, sale de el, y vuelve al estado inicial en + numero de pasos.
Sean i y j estados de una cadena de Markov Xn; Definimos fij^(n) como la probabilidad de que empezando en xo=i, visita el estado j en el n paso.
Es decir:
fij^(n)=P{xn=j/ xk es distinto de j k=1…n-1 xo=i}
fij^(1)=Pij y fij(0)=0
Se puede ver que la probabilidad de ir de i a j en n pasos satisface:

Pjj^(n) Probabilidad de xn=j dado que xo=j
Pij^(n) es ir de i a j en n pasos aunque se pudo haber visitado j antes
Fij^(n) es ir de i a j en n pasos sin haber visitado j antes.
Diremos que i es en estado recurrente si fii=1; y que i es transitorio si fii<1 onblur="try {parent.deselectBloggerImageGracefully();} catch(e) {}" href="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj_OUWc-a8X_fK8z3kYH5OFCMHKV2zfi88mAQyT9FS3pWGLNx78n093rM2dsQZAIk5Fov7lwCdmco5OZuwoCkR8JYZQbsCrUeHurpzI1DPzpGpVMmLSu5_R1eZrd8Gqml2WWRk37HNq7EJW/s1600-h/Dibujo.jpg">

Una cadena de Markov que consta de una y solo una clase comunicante se le llama cadena irreducible, equivalentemente la cadena es irreducible si cualquier par de estados son comunicantes.
Periodicidad: el periodo d(i) de un estado i como el máximo común divisor de todos los enteros n>=1 para los cuales Pij^(n)>0 probabilidad de que regrese al edo.
Si Pij^(n)=0 para todo n>=1 d(i)=0
Si d(i)>0 i es un estado periódico con periodo d(i) mientras que si el periodo d(i) =1 decimos que i es un estado aperiódico (llega una vez y no vuelve a regresar)
2 estados están en la misma clase de equivalencia si y solo si i y j son comunicantes.
Un estado i es absorbente si y solo si Pii=1 por lo tanto Pij=0
Ejemplo:

El estado 1 es absorbente, el estado 2 puede quedarse en 2 o pasar al estado 1, el estado tres puede ir al estado 1 quedarse igual o pasar el estado 4, y el estado 4 puede pasar a todos los estados.
Entonces: C1= 1 y es absorbente
C2 =2 C3 =3,4
Si i es recurrente y i<->j entonces j es recurrente.
Si un proceso regresa un número infinito de veces al estado i, entonces, que regrese a j en un número infinito de veces pues son recurrentes, entonces regresa a i con probabilidad de 1 y entonces regresa a j con probabilidad de 1.
Nota: El patrón de comportamiento de regresar a i no es el mismo patrón de ir a j.
Si j es un estado transitorio, el número esperado de transiciones de i a j para cualquier estado inicial xo =i es finito, esto es:

Para toda i
Cuando n tiende a infinito, el proceso deja de visitar a j y entonces se dice que j esta en estado transitorio.
Ejemplos:
Periódicos: lluvias en algunos estados
Recurrentes: huracanes, fenómeno del niño, ventas de productos.
Mij tomara los valores de:
a) Infinito si j es transitorio o
b) Si j es recurrente Mjj=

Se llama tiempo medio de recurrencia de i y representa el tiempo de retorno al estado j (tiempo de regreso a j)
Si se quiere estimar el periodo de un estado recurrente se haría con el promedio.
nfjj es un promedio ponderado
Si i <-->j entonces lim 1/n ΣPij = 1/ Mjj
Lim Pij^(n) = 1/Mjj si j es aperiódico
J es Periodico con periodo d si : el limite cuando n tiende infinito:
Lim Pij^(d)= d/Mjj
Si j es un estado recurrente decimos que j es recurrente positivo si Mjj< mjj =" infinito." d="d(j)">=1 es el periodo de j entonces:
Πj= lim Pij(n,d)=d/Mjj
Entonces j es recurrente positivo si Πj >0 y recurrente nulo si Πj =0
Un estado aperiódico y recurrente positivo se dice que es ergodico ( o sea si el proceso vista el estado una vez y no regresa en el mismo periodo y el tiempo promedio de vista es infinito.
Recurrente: vista el edo y tiene probabilidad >0 de volver a visitarlo en k pasos.
Periódico: vista el proceso en el mimo numero de pasos.
La distribución Poisson

Proceso de Poisson x= {N(t); t>0} es un proceso de poisson con intensidad media λ con λ>0 si:
a)X tiene incrementos independientes es decir, 0
o sea x(t+h)-x(t) tiene una distribución Poisson con parámetro λh
Con esperanza (media) λh, y varianza λh
Ejemplo:
El numero de personas que llegan a una tienda sigue un proceso Poisson con media λ=4 (personas por hora) dado que la tienda abre a las 9 am , cual es la probabilidad de que exactamente un cliente haya llegado a las 9:30 y de que un total de 5 clientes hayan llegado a las 11:30?
El proceso empieza a las 9
P={N(1/2)=1, N(5/2)=5} ( el primero cuenta la primera parte y el segundo la segunda parte)
Como son independientes:
P(N(1/2)=1 * P(N(5/2)-N(1/2)=4)
Entonces esto es igual a Poisson λ=4 y n=1 * n=4 = 0.1549
Cuando λ es variable sea tn del tiempo son procesos de Poisson no homogéneos.
Los eventos ocurren aleatoriamente en el tiempo y sea N(t) el numero de eventos que ocurren en el intervalo de tiempo (0,t) se dice que el proceso estocástico {N(t) t>0} es un proceso de Poisson de intensidad λ si:
1.- N(0)=0
2.,-N(t) tiene incrementos independientes y estacionarios
3.-P{N(h)=1}= λh+O(h)
4.-P{N(h)>=2}=O(h)
Ejemplo:
El numero de vehículos que pasan por cierta intersección en el intervalo de tiempo (0,t) sigue un proceso Poisson con E(N(t))=3t en donde la unidad de tiempo son minutos.
a) Encontrar la probabilidad de que al menos 2 vehículos pasen durante cualquier minuto.
b) Sea A) que al menos 4 vehículos pasan durante el primer minuto y B) a lo mas 2 vehículos pasan durante el 2do minuto, encuentre la probabilidad de que ambos eventos (A y B ocurran)
a)Es un proceso estacionario de distribución que conozco.
P{N(t)>2}=1-P(N(t)<2 h="1" 3=".80">=4}=1-(P=0+P=1+P=2+P=3) λ=3 h=1
B) P{N(2)<=2}= P(N(2)=0+P(N(2)=1+P(N(2)=2) λ=3 h=1 Sean T1, T2, T3….Tk variables aleatorias independientes exponencialmente con media 1/λ Pero quiero la distribución del tiempo acumulado, por lo tanto: T=ΣTi k>=1 ; y T se distribuye como una funcion Gama (1/λ,k)
Proceso de Poisson no-homogéneo
Si λ ya no es una constante, es decir ya no es un proceso estacionario, λ es una función del tiempo y varia en el intervalo en el que sucede el proceso.
En el intervalo (s,t) X(t)-X(s) es el numero de eventos que ocurrieron en el intervalo X es un proceso de poisson ( Conteo)
Ahora como ya no es estacionario λ se encuentra como:
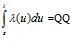
X(t)-X(s) se distribuye como un proceso Poisson pero con parámetro QQ pues λ es dependiente del tiempo.
Ejemplo:
La demanda de primeros auxilios en un determinado lugar ocurre de acuerdo con un proceso poisson no homogéneo con la siguiente función de intensidad.
λ(t)= 2t si 0<=t<=1 ; 2 si t esta entre 1 y 2 ; y 4-t si t esta entre 2 y 4. Donde t es media en horas a partir del momento que abre el puesto de auxilios. Cual es la probabilidad de que ocurran 2 demandas de auxilio en las 2 primeras horas y 2 en las segundas 2 horas. Son independientes P(1er)*P(2do) Entonces para las 2 primeras horas: Mx=∫1 02t dt +∫2 12dt= 1+2=3 P(N(2)=2 = e-332/2!= .2240 Para las segundas 2 horas: Mx=∫1 4-t dt =4(4-2)-4(42-22)=2 P(N(4)-N(2)=2)=P(N(2)=2)= e-222/2!=.2706 Sean Wt el tiempo en el cual se vista el estado N(t), entonces Sn=Wn+1-Wn es el tiempo de permanencia.
Sn cuenta el tiempo que el estuvo constante el proceso. So no cuenta con nada; S1 cuenta 1 evento.
EL tiempo de espera Wn tiene una distribución gama cuya función de densidad es:
Fwn(t)=

Procesos Continuos
Proceso de Winey o Movimientos Browniano
X={x(t),t>=0} es un proceso de Winey si:
a) x(0)=0
b) x(t) tiene incrementos independientes estacionarios con x(t+h)-x(t) ~N(0,σ2h)
Si σ2=1 decimos que x es un proceso de Winey estándar y nos referimos a el como
{B(t); t>=0}~N(0,h)
Si el proceso no es estándar entonces se estandariza.
Variaciones del Proceso Browniano
Movimiento Browniano con tendencias
Decimos que x(t) es un movimiento browniano con tendencias en el coeficiente µ y parámetro de varianza σ2 si:
X(0)=0
X(t) , t>=0 tiene incrementos independientes y estacionarios
X(t) se distribuye como una normal con media µ y varianza σ2t
La variación no es estacionaria, sino que cambia con el tiempo.
Movimiento Browniano Geométrico
Si {u(t), t>=0} es un movimiento browniano con tendencia entonces el proceso x(t)>=0 definido por: x(t)=ey(t) se llama movimiento browniano geometrico.
Se dice que el proceso estocastico X(t) es débilmente estacionario si:
Var (xt) =σt < infinito par toda t ; µt=µ para toda t ; cov(x(t) x(s)= cov(x(t+n) x(s+n) para toda s, t, n.
Si es estrictamente estacionario entonces débilmente estacionario entonces tiene la misma distribución entonces tienen la misma media y varianza finita.






